(This work was done in collaboration with Prof. Rui Castro and Prof. Robert Nowak.)
Download information: ctftoolbox_linux64 ctftoolbox_mac ctftoolbox_windows. If you have a different platform than one of those listed above, download the Mac or Linux toolbox and run the “compile.m” script to generate the appropriate MEX files. To install, download the appropriate toolbox for your platform, unzip it to the desired location, and add that location to your MATLAB path. To get started, try running Example_CTFWedgeletApprox.m and Example_CTFPlateletApprox.m. This toolbox contains C mex files to be used with MATLAB for coarse-to-fine wedgelet and platelet image reconstruction under Poisson or Gaussian noise models. The method requires O(N) computation time.
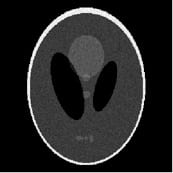
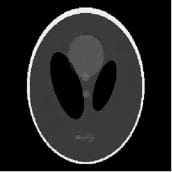
For wedgelet image reconstruction, we consider a sequential, coarse-to-fine estimation of a piecewise constant function with smooth boundaries. Accurate detection and localization of the boundary (a manifold) is the key aspect of this problem. In general, algorithms capable of achieving optimal performance require exhaustive searches over large dictionaries that grow exponentially with the dimension of the observation domain. The computational burden of the search hinders the use of such techniques in practice, and motivates our work. We consider a sequential, coarse-to-fine approach that involves first examining the data on a coarse grid, and then refining the analysis and approximation in regions of interest. Our estimators involve an almost linear-time (in two dimensions) sequential search over the dictionary, and converge at the same near-optimal rate as estimators based on exhaustive searches. Specifically, for two dimensions, our algorithm requires O(n^{7/6}) operations for an n-pixel image, much less than the traditional wedgelet approaches, which require O(n^{11/6}) operations. The coarse-to-fine platelet image reconstruction technique is similar, but can be used to estimate images consisiting of (C2) smooth surfaces separated by (C2) smooth boundaries.
 |
 |
 |
| Noisy Image, MSE = 0.01003 | Coarse Estimate, MSE = 0.1603 | Image Estimate, MSE = 0.004885 |
 |
 |
 |
| Noisy Image, MSE = 0.009025 | Coarse Estimate, MSE = 0.001174 | Image Estimate, MSE = 0.0002264 |