(This work was done in collaboration with Dr. Robert Nowak.)
Download information: Toolbox, 3D Toolbox
To install, download the appropriate toolbox for your platform, unzip it to the desired location, and add that location to your MATLAB path. To get started, try running Example_1D.m, Example_2D.m, Example_2D_Gaussian.m, and Example_Tomography.m. This toolbox contains MATLAB code for translation invariant Poisson or Gaussian signal and image reconstruction. The method requires O(N log N) computations.
Poisson image denoising example:
The techniques presented here allow multiscale photon-limited image reconstruction methods to be implemented with significantly less computational complexity than previously possible. Multiscale Haar estimation is a promising technique in the context of Poisson data, but the computational burden it imposes makes itimpractical for many applications which involve iterative algorithms, such as deblurring and tomographic reconstruction. With the advent of the proposed implementation techniques, hereditary translation-invariant Haar wavelet-based estimates can be calculated in O(N logN) operations; this complexity is comparable to that of standard translation-invariant wavelet denoising (O(N logN)). Fast translation-invariant Haar denoising for Poisson data is accomplished by deriving the relationship between maximum penalized likelihood tree pruning decisions and the undecimated wavelet transform coefficients.
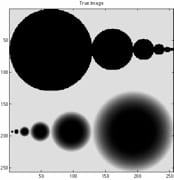 |
 |
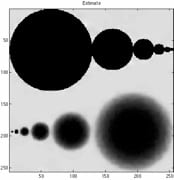 |
| Original | Observation | Reconstruction |
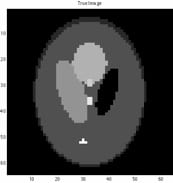 |
 |
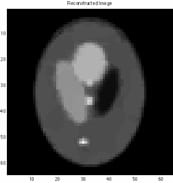 |
| Original | Observation | Reconstruction |
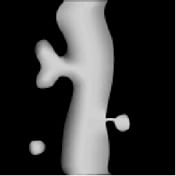 |
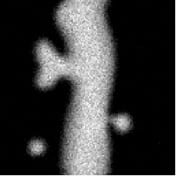 |
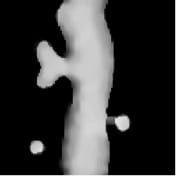 |
| Original | Observation | Reconstruction |