Introduction
This page contains a summary and code associated with the paper “Changepoint detection for high-dimensional time series with
missing data”, by Y. Xie, J. Huang, and R. Willett. In IEEE Journal of
Selected Topics in Signal Processing, vol. 7, no. 1, 2013. arXiv:1208.5062
This page describes a novel approach to change-point
detection when the observed high-dimensional data may have missing
elements. The performance of classical methods for change-point
detection typically scales poorly with the dimensionality of the data,
so that a large number of observations are collected after the true
change-point before it can be reliably detected. Furthermore, missing
components in the observed data handicap conventional approaches. The
proposed method addresses these challenges by modeling the dynamic
distribution underlying the data as lying close to a time-varying
low-dimensional submanifold embedded within the ambient observation
space. Specifically, streaming data is used to track a submanifold
approximation, measure deviations from this approximation, and
calculate a series of statistics of the deviations for detecting when
the underlying manifold has changed in a sharp or unexpected manner.
The proposed approach leverages several recent results in the field of
high-dimensional data analysis, including subspace tracking with
missing data, multiscale analysis techniques for point clouds, online
optimization, and change-point detection performance analysis.
Simulations and experiments highlight the robustness and efficacy of
the proposed approach in detecting an abrupt change in an otherwise
slowly varying low-dimensional manifold.
Goal: Online tracking of a manifold M_t
Assumption: low dimensional manifold, slowly time-varying
Observation: high dimensional data
Tracking: using a sequence of low-dimensional approximations
Motivation: modeling high-dimensional time series: video, evolving social networks, network traffic, etc.
Problem Setup
Observation: x_t=v_t+w_t,v_t\in\mathcal{M}_t,\mathcal{M}_t\subset\mathcal{R}^D
Union of Subspaces: $\widehat{\mathcal{M}}_t=\bigcup_{(j,k)\in\mathcal{N}_t} S_{j,k,t}$, Complexity: $K_t=\left|\mathcal{N}_t\right|$
$S_{j,k,t}=\left\{ v\in\mathcal{R}^d:~v=U_{j,k,t}\beta+c_{j,k,t} \right\}$
Parameters: subset $\left\{U_{j,k,t},c_{j,k,t},\Lambda_{j,k,t} \right\}$, deviate: $\delta_{j,k,t}$
Tree Representation:
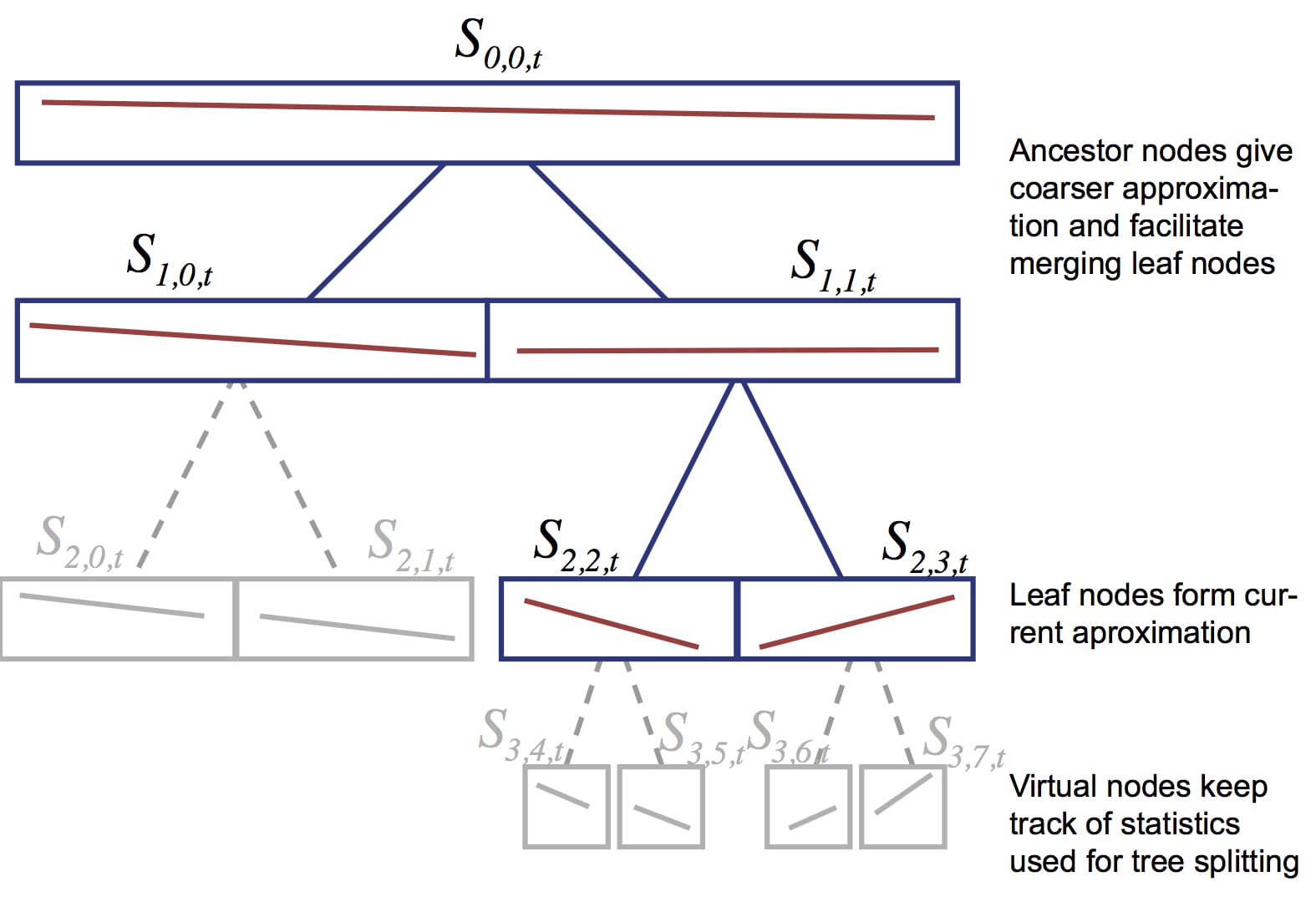
Full package of MOUSSE can be downloaded here.
Initialization
Recursively perform bi-partition of a batch of training samples. For each partition, do eigendecomposition to initialize a corresponding node in the tree. The obove process will be stopped when a parition’s error $\delta(D-d)$ is less than a threshold. Then an extra partition will be employed to initialize the virtual nodes.
Online Update of Tree
Projection: $\beta=U^T(x_{t+1}-c_t)$
Residual: $\beta_\perp=(x_{t+1}-c_t)-U\beta$
Classify a sample to subset: approximation Mahalanobis distance $d(x,S)=\beta^T\Lambda^{-1}\beta+\delta^{-1}\|\beta_\perp\|^2$
Update Subsets: Update the set with minimum distance $d(x_{t+1},S_{j,k,t}),~(j,k)\in\mathcal{N}_t$ and its ancestors and minimum-distance virtual node.
Center: $c_{t+1}=\alpha c_t+(1-\alpha)x_{t+1}$
Spread: $\Lambda_{t+1}^{(m)}=\alpha\Lambda_{t}^{(m)}+(1-\alpha)\|\beta^{(m)}\|^2$
Deviate: $\delta_{t+1}=\alpha\delta_t+(1-\alpha)\|\beta_\perp\|^2/(D-d)$
Basis: Several ways to update orthonormal basis $U_{t+1}$: GROUSE [1], PETRELS [2] with standard orthonormalization and fast orthonormalization [3].
Tree Structure Updating
Premise: balancing approximation error with complexity $log(K_t)$
Pruning: merge leaves of tree, approximation error $\nearrow$
Growing: turn two virtuals into leaf nodes, initialize virtual nodes by scale $\Lambda^{(1)}$ by 1/2, approximation error $\searrow$
Tracking Manifold Example
The video shows a $D=100$ but $d=1$ manifold by projecting it onto a 3D space. Each observation has about 40% missing entries, ie, about 40 of the 100 dimensions are not observed. Dataset and code generating this video can be downloaded here.
Application in Anomaly Detection
Detect anomaly in solar flare video. There is an obvious anomaly at about $t=227$. Full dataset and code generating this video can be downloaded here.
References
[1] L. Balzano, R. Nowak and B. Recht, “Online identification and tracking of subspaces from highly incomplete information,” in proceedings of the Allerton Conference on Communication, Control and Computing, Sept. 2010, pp. 704-711.
[2] Y. Chi, Y. Eldar, and R. Calderbank, “PETRELS: subspace estimation and tracking from partial observations,” IEEE. Conf. on Acoustic, Speech and Signal Processing, 2012.
[3] K. Abed-Meraim, A. Chkeif and Y. Hua, S. Attallah, “On a class of orthonormal algorithms for principal and minor subspace tracking,” Journal of VLSI Signal Processing, 2002, vol. 31, pp. 57-70.