1. Quantum Error Correction and Noise Mitigation

Qubit errors, gate errors and the high cost of quantum error correction present significant challenges to the practical adoption of quantum computing. Our group has been developing improved error correction codes, decoders, noise mitigation techniques, and optimizations across quantum computing stacks. For example, we demonstrated lightweight parity checking, minimized gate and algorithmic errors in Hamiltonian simulations, and performed hardware-specific optimizations that decreased SWAP and Toffoli gate errors by 40% compared to a native compiler. In earlier work we also developed the maximum likelihood decoder for the surface quantum error correction code. The use of simulators and quantum computers, including superconducting qubits, neutral atom arrays, and ion traps, has been integral to demonstrating the benefits of our work.

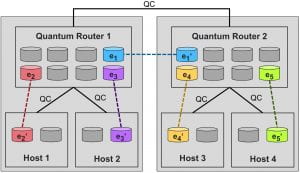
2. Quantum Communication and Networking

Recent experimental advances make quantum communication networks a reality. Our research focuses on quantum network architectures, the control protocol stack, and optimizations of entanglement distribution protocols with focus on improving throughput and entanglement fidelity. Our team also developed the Simulator of QUantum Network Communication (SeQUeNCe), an open-source tool available on GitHub, capable of performing photon-level simulations of optical quantum networks with picosecond resolution. This work motivated experimental efforts to build entanglement distribution networks. For example, in collaboration with the Zhong lab, we built an experimental network testbed that achieves high throughput by varying photon arrival times and a 20ps absolute timing synchronization without the need for a dedicated synchronization channel.

3. Quantum Computing Applications

We have been using quantum computers and quantum simulators to demonstrate applications in computational chemistry, optimization, and machine learning. These demonstrations often required the use of algorithmic optimizations, approximations, or simulations on high-performance computers. A few highlights of our work include optimizations of the variational quantum eigensolver algorithm that yielded 8-30x lower cost, and a method for preparing arbitrary quantum states yielding exponentially shallower circuits required for data encoding in machine learning. Some of our demonstrations were enabled by techniques we developed to extend the size of quantum systems that can be simulated, such as tensor slicing, matrix product states, and quantum circuit partitioning.