Transition-based models are a relatively empirically-accessible alternative to traditional population dynamics-based models of ecological communities. In this approach, study objects, such as points in space, are characterized by their ecological state, such as the species or size class of organism present, whether or not an organism is present, some combination of species present, or nutrient status. The study objects are then repeatedly censused over a defined interval, yielding a time series of the states that each object is in. These can then be organized into transition probabilities, which can then be related to different ecologically and mechanistically-relevant conditions of the system, such as the prior state(s) of the object or the state of nearby objects. Because data can be taken over relatively small areas, the functions describing transitions are generally not complex, and the structures often have well-understood analytical properties or are easily simulated by computer, these models are some of the easiest for empiricists to parameterize and analyze, so have the best chance of being applied to complex ecological communities if they can provide useful information. Although they lack the mechanistic details of other more commonly used models, the way in which categories are chosen can reflect important mechanisms, and at a minimum they can help focus our attention on key areas of the ecosystem to study in more detail. A key unresolved question is whether these frameworks can make useful predictions in ecological systems. In many cases, these models have initially been applied to forest systems, which are virtually impossible to subject to experimental test. Consequently, I have been exploring transition-based approaches in rocky intertidal communities, where I can carry out rigorous experimental tests of them.
Starting in 1993 I have been accumulating a dataset of transitions on the wave-exposed shores of Tatoosh Island, Washington, most of which are recorded on 60 x 60 cm grids of 100 points each, permitting analysis of spatial relationships over small scales. This census program generates ~1700 transition data points each year (by comparison, each plot generating 100 transition data points generates only 1 data point to parameterize models based on population dynamics each year). In parallel, I also have maintained a long-term replicated experiment excluding the dominant sessile species in the community, the mussel Mytilus californianus, to use as a rigorous test of different transition-based models parameterized in unmanipulated areas.
Top: species abundance distribution predicted by the NTB (dashed) vs. observed (solid). Bottom: species abundances predicted vs. observed in experimental data.
One question that I have addressed is whether it is even important to account for species differences and how they shape species interactions (Wootton 2005). The Neutral Theory of Biodiversity has received much recent attention because it is based on basic principles of population dynamics and is capable of generating patterns similar to broad-scale relationships seen in communities (e.g., species-area and abundance-frequency distributions). A key and controversial assumption of this model is that all species competing for a limiting resource are ecologically equivalent. Although the model is dynamically based, prior evidence supporting the model depended on the ability of the model to generate static patterns similar to those seen in real communities. The dynamics of the model are readily translated to transitions of species using units of limiting resources, particularly when the limiting resource is space, hence the intertidal dataset provides an exceptional opportunity to parameterized the dynamical equations underlying the neutral model, and a unique opportunity to rigorously test it with the parallel experimental mussel removal. As in other systems, the neutral model can capture the static abundance-frequency distribution of species in the intertidal zone and in the experimentally manipulated plots, suggesting that the community could be neutrally organized. Because I was able to parameterize the dynamics of the model, however, I could make strong predictions about the identity of the species contributing to each abundance category, predictions which matched poorly the results from the experiment. Hence, species differences are critical to make accurate predictions of the system, and studies hoping to determine whether neutral dynamics apply in other communities must use more stringent criteria. Current research is exploring whether the framework of the neutral theory can be adapted to accommodate species differences and generate accurate predictions of the system response to experimental manipulation.
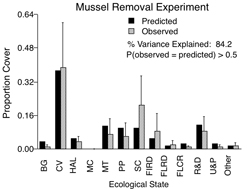An alternative framework that accounts for species differences is the multi-species Markov chain model. This framework is based on a simple matrix of transitions from ecological state to another, with transitions depending only on the prior state of each study object. I also parameterized this model with my transition data and analyzed it thoroughly to determine predicted effects of species extinction and sensitivity of the community to different transitions (Wootton 2001a, 2001b). I then challenged the model to make predictions about changes associated with several novel situations (changes in habitat orientation, experimental removal of bird predators and mussels) and found remarkably good quantitative agreement in species composition between model predictions and empirical results (Wootton 2001b, 2004). This represents one of the first successful attempts to parameterize any form of multi-species model and then quantitatively predict the effects of extinction in a natural, complex multi-species system. I am now applying this framework to other systems, particularly those with mobile species. Using clustering methods to identify different ecological states in samples of multiple individuals, I have applied the approach to zooplankton communties in Carpenter and Kitchell’s study lakes, and have found that Markov models developed for low planktivory/high piscivory conditions can predict reasonably well the change in the community in high planktivory/low piscivory conditions.
Although capable of predicting species composition of the system, Markov chain models cannot recreate another striking feature of intertidal (and other) landscapes: patchy spatial structure. Consequently, I have been parameterizing and exploring spatially-explicit extensions of the model that account for localized interactions among organisms: cellular automata models. These models have received much recent attention in a variety of fields because they are capable of generating complex patterning (‘self-organized critical behavior’) at large scales from relatively simple rules about how objects interact locally. Most of these results come from theoretical simulations of hypothetical situations and involve only a limited number of possible states (typically 3). But do models with parameters derived from real systems and with many more possible states show similar behavior? Can we successfully scale up an understanding of small-scale interactions to generate large-scale patterning? I addressed these questions using my transition-based data for the intertidal zone by developing a cellular automaton model in which transitions depended on the state of neighboring points (Wootton 2001c). Under the most realistic formulation of the model (with 15 species states, and a dual timescale of local interactions with rapidly propagating disturbance transmitted by mutual attachment of mussels to their neighbors combined with slower neighbor-dependent species replacement processes) the large-scale patterning of the system was successfully predicted. The results indicate that scaling up from small-scale intensive studies of ecological process may indeed permit making large-scale predictions, and supports suggestions that strong patterning in nature requires a combination of fast, small-scale positive feedback processes that are counteracted by slow large scale negative feedback mechanisms. I am currently interested in exploring ways to collect and analyze larger-scale multi-species data on spatio-temporal dynamics of ecosystems on larger scales, and methods to more effectively uncover multiple spatially-local dependencies among species (the current model only considers local relationships involving mussels).
